O processo de "matematização" do homem sobre a representação da natureza (Parte 1/2)

        Ao longo dos tempos, os humanos se dedicaram a observar os padrões correspondentes à forma como a natureza lhes apresentava na sua originalidade. Nesse cenário, o desenvolvimento de técnicas para melhor análise de tais níveis de apresentação se tornou indispensável. Para muitos artistas, arquitetos e estudiosos da anatomia humana, a utilização dessas estratégias, compreendidas majoritariamente nas Ciências Exatas, significa o modo mais próximo do perfeito para se dedicar aos seus projetos. Nesses termos, explica-se a presença massiva da proporção áurea (número de ouro, entendido na sequência de Fibonacci) durante séculos em clássicos da pintura, memoráveis estruturas arquitetônicas e na determinação do belo no referente aos corpos humanos (ver Figura 1, 2 e 3, correspondentes à pintura Mona Lisa, Parthenon e o Homem Vitruviano).

Figura 1 – Mona Lisa e Proporção Áurea. Imagem retirada da internet: Disponível em: < http://style.tribunnews.com/2017/08/25/3-lukisan-ini-ternyata-menyimpan-fakta-dan-rahasia-padahal-terkenal-tapi-bikin-ngeri-juga >. Acessado em mar. 2018.

Figura 2 – Parthenon (Grécia) e Proporção Áurea. Imagem retirada da internet: Disponível em: < http://pre.univesp.br/o-numero-de-ouro-e-a-divina-proporcao#.WrfOy4jwbIU >. Acessado em mar. 2018.

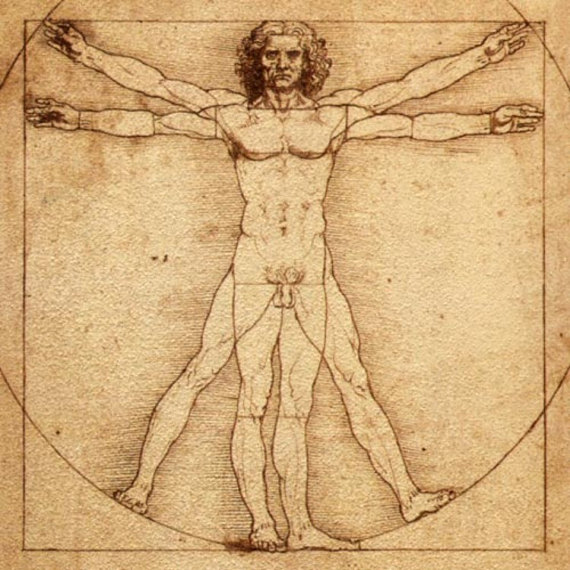Figura 3 – Homem Vitruviano. Imagem retirada da internet:  Disponível em < https://www.etsy.com/listing/71585300/vitruvian-man-cross-stitch-pattern-pdf >. Acessado em mar. 2018

        Estima-se que a primeira vez que a proporção áurea foi observada tenha sido pelo matemático grego Hípaso de Metaponto (470 – 400 a.C.), o principal responsável por profundas mudanças no pensamento filosófico da escola pitagórica (Ferrer, 2005). A descoberta da incomensurabilidade por Hípaso, verificada no valor da diagonal de um quadrado de lado unitário, da base de um triângulo isósceles retângulo ou ainda da razão entre diagonal e lado do pentágono regular, induziu a análise da proporção áurea, representada pela letra grega φ (PHI) equivalente a aproximadamente 1,618. Nesse sentido, tomando uma das formas de apurar o caráter incomensurável da matemática, percebe-se que, quando se inscreve uma estrela de 5 pontas a partir dos vértices de um pentágono regular, surge um novo pentágono regular como consequência do cruzamento das diagonais do primeiro (ver Figuras 4, 5 e 6, registros da realização do pentágono e da estrela que o inscreve pelo discente e pelos integrantes do seu grupo). Conclui-se, ainda, a presença de proporcionalidade segundo o número de ouro tanto entre as partes das diagonais componentes da estrela quanto entre os pentágonos regulares formados (ver Figuras 7 e 8, explicativas da proporcionalidade áurea).

Figura 4 - Estrela de 5 pontas circunscrita segundo a Proporção Áurea. Conteúdo da imagem: Eugênio Daniel Magan, Ingrid Loyola e Istael Borges. Registro da Imagem: Ingrid Loyola (28 de fev. 2018)

Figura 5 - Estrela de 5 pontas circunscrita segundo a Proporção Áurea e seus produtores. Registro da Imagem: Desconhecido (28 de fev. 2018)

Figura 6 - Estrela de 5 pontas circunscrita segundo a Proporção Áurea e seus produtores. Registro da Imagem: Istael Borges (28 de fev. 2018)

Figura 7 - Pentágono Regular ABCDE (em rosa), a primeira Estrela de 5 pontas formada pelo intercruzo das diagonais do pentágono maior (em azul claro), Pentágono Regular A'B'C'D'E' (em lilás) formado pela primeira estrela, a segunda Estrela de 5 pontas (em verde) e o último Pentágono Regular (em amarelo). Imagem produzida pelo discente em março de 2018.

Figura 8 - Explicação, segundo Hípaso, da incomensurabilidade da matemática através da relação, que posteriormente será definida como Áurea, entre a diagonal do Pentágono Regular e seu lado. Para fins de unidades de comprimento, no fim do desenvolver da explicação, utiliza-se somente resultados compreendidos no Conjunto dos Números Naturais. Imagem produzida pelo discente em março de 2018.

Nota: 

Esta publicação está dividida em duas partes, por escolha de seu autor. Para continuar a leitura, basta clicar no link abaixo ou pesquisar no próprio espaço do blog "O processo de 'matematização do homem sobre a representação da natureza (PARTE 2/2).

Link < https://alias17.blogspot.com.br/2018/03/o-processo-de-matematizacao-do-homem_6.html >.